군집분석
- 군집분석이란 객체의 유사성을 측정해서 유사성이 높은 집단끼리 분류하는 통계기법
- 머신러닝 분야에서 이상치 탐지를 위해 사용되기도 함
- 대표적인 비지도 학습
- 계층적 군집분석과 비계층적 군집분석으로 나뉨
[군집분석 vs 요인분석]
| 구분 | 내용 |
| 군집분석 | - 객체간의 상이성을 규명 - 군집의 특성 파악 |
| 요인분석 | - 유사한 변수를 묶어 다중공선성을 줄이기 위함 |
[계층적 군집분석]
- n개의 군집으로 시작해 점차 군집의 개수를 줄여나가는 방식
- 군집의 거리를 계산하는 방법에 따라 연결법이 달라짐
- 모든 객체는 거리 행렬을 통해 가까운 거리의 객체들의 관계를 규명, 군집 개수 선택
- 연결법
| 구분 | 내용 |
| 최단연결법 | - 거리행렬에서 거리가 가장 가까운 데이터끼리 묶어서 군집 형성 |
| 최장연결법 | - 데이터와의 거리를 계산할때 최장거리로 계산 |
| 평균연결법 | - 데이터와의 거리를 계산할때 평균거리로 계산 |
| 중심연결법 | - 두 군집간의 거리를 두 군집의 중심 간 거리로 계산 |
| 와드연결법 | - 군집 내 편차들의 제곱합에 근거를 두고 군집화 - 데이터의 크기가 너무 크지 않다면 가장 많이 사용 - 군집 내 편차는 작고 군집간 편차는 크게 군집화 - 계산량이 많은 단점이 있지만 군집 크기를 비슷하게 만듬 - 해석력이 좋음 |
- scipy.cluster.hierarchy.linkage(parameters)
- scipy.cluster.hierarchy.dendrogram(parameters)
scipy.cluster.hierarchy.linkage — SciPy v1.12.0 Manual
For method ‘single’, an optimized algorithm based on minimum spanning tree is implemented. It has time complexity O(n2). For methods ‘complete’, ‘average’, ‘weighted’ and ‘ward’, an algorithm called nearest-neighbors chain is imple
docs.scipy.org
- scipy.cluster.hierarchy.fcluster(parameters)
scipy.cluster.hierarchy.fcluster — SciPy v1.12.0 Manual
An array of length n-1. monocrit[i] is the statistics upon which non-singleton i is thresholded. The monocrit vector must be monotonic, i.e., given a node c with index i, for all node indices j corresponding to nodes below c, monocrit[i] >= monocrit[j].
docs.scipy.org
예시) USArrests정보로 최단, 와드연결법 실시
- 데이터로드 및 전처리
#컬럼명 변경
us.rename(columns={"Unnamed: 0": "state"}, inplace=True)
#컬럼명 소문자로
us.columns = us.columns.str.lower()
us.head()- 최단연결법
- 거리계산은 유클리드거리로 진행
- t값을 기준으로 군집화를 실시했을때 총 6개의 군집이 생기는 것을 확인
- 1개의 state가 1개의 군집으로 모인것도 있음을 확인
#군집분석
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt
#연결방법: 최단연결, 거리계산방법: 유클리드
single = linkage(
us.iloc[:, 1:],
metric="euclidean",
method="single"
)
#시각화
plt.figure(figsize=(10, 7))
dendrogram(
single,
orientation="top",
labels= us["state"].tolist(),
color_threshold=25,
distance_sort="discending"
)
plt.axhline(y=25, color="r", linewidth=1)
plt.show();
- 와드연결법
- 최단 연결법은 군집이 가지고 있는 객체 수가 비슷하지 않아 군집 해결에 어려울 수 있음
- 이런 문제점을 보완하기 위해 와드연결법을 사용
- 유클리디안 거리를 이용해 와드연결법 실시
- t=250선에서 수평축을 그려보면 군집이 3개로 나누어짐을 알 수 있음
- 각 군집의 객체 수도 비슷함을 알 수 있음
#와드연결법 실행
ward = linkage(
us.iloc[:, 1:],
metric="euclidean",
method="ward"
)
plt.figure(figsize=(10, 7))
dendrogram(
ward,
labels=us["state"].tolist(),
distance_sort="descending",
orientation="top"
)
plt.show();
- 군집이 확인 되었으니 fcluster함수를 이용해 각 객체들이 가진 군집번호 데이터화
#각 군집 데이터화
cluster_label = fcluster(ward, 250, criterion="distance")
cluster_label
#원 데이터에 파생변수로 할당된 클러스터 삽입
us["cluster"] = cluster_label
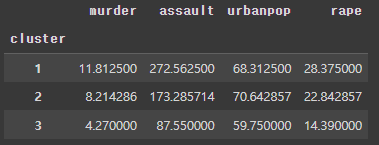
us.head()- 클러스터별 평균 파악
- 1번 클러스터: murder, assault, rape의 평균이 다른 클러스터에 비해 높음
- 2번 클러스터: 전체적으로 중간치의 특성을 보임 urbanpop의 평균이 가장 높음
- 3번 클러스터: 전체적으로 낮은 특성을 보임
[비계층적 군집분석]
- 랜덤하게 군집을 묶어가는 알고리즘
- 거리를 계산하는 방식으로 군집화 실행
- 대표적으로 K-means, DBSCAN, 혼합분포 군집분석이 있음
1. K-means
- 속성의 수가 적은 단순한 데이터에 주로 활용
- 주어진 데이터를 k개로 군집화하며 각 클러스터와 거리차이의 분산을 최소화 하는 방식으로 작동(k개는 연구자 마음)
- 변수가 많을 경우 군집화의 정확도가 떨어짐 > pca(차원축소)를 실시해야 함
- 군집화 알고리즘
- 초깃값 설정: k(군집 수)를 설정할 경우 k개의 데이터를 중심점으로 설정
- 클러스터 설정: 각 데이터로부터 중심점까지를 유클리드 거리로 계산해 해당 가장 가까운 클러스터로 데이터를 재할당
- 각 클러스터의 무게중심을 재설정
- 위의 과정을 반복하다가 중심 변화가 작을때 알고리즘 반복 중지
- 최적의 군집 개수 판단 방법
- 콜린스키 하라바츠 스코어
- 모든 클러스터에 대한 클러스터 간 분산과 클러스터 내 분산의 합의 비율
- 높을 수록 좋음
- 엘보우
- 컬러스터 내 오차제곱합(SSE)을 개수마다 비교하는 방법
- 반복문을 통해 클러스터 개수(k)를 늘려가며 SSE값을 비교
- 기울기가 소실되는 구간을 elbow로 판단하고 그 순간을 최적의 클러스터 개수로 판단
- 콜린스키 하라바츠 스코어
예시) iris데이터를 활용한 군집 분석
- 데이터정의
- 최적의 군집 수 결정
- 하라바츠스코어
- 3개가 최적의 군집수로 보임
- 하라바츠스코어
#군집 수 결정(하라바츠스코어)
from sklearn.metrics import calinski_harabasz_score
import warnings
warnings.filterwarnings("ignore")
for k in range(2, 10):
km = KMeans(n_clusters=k, random_state=1)
km.fit(df)
labels = km.labels_
print(k, calinski_harabasz_score(df, labels))
'''
2 513.9245459802768
3 561.62775662962
4 530.4871420421675
5 495.54148767768777
6 473.5154538824768
7 443.84523107907245
8 440.59767319067873
9 407.0468400265113
'''
-
- 엘보우
- 시각화 결과 2개에서 3개가 기울기가 완만해 지는 지점임
- 엘보우
#엘보우 확인
import matplotlib.pyplot as plt
sses = []
for k in range(1, 11):
km = KMeans(n_clusters=k, random_state=1)
km.fit(df)
sses.append(km.inertia_) #kmeans의 sse 확인 메서드
plt.plot(range(1, 11), sses, marker="o")
plt.xlabel("n_clusters")
plt.ylabel("SSE")
plt.show();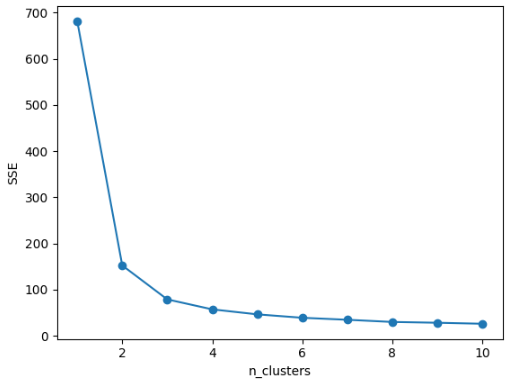
- 군집분석 실시
- k=3으로 군집분석 실시 후 groupby, 시각화
- 변수별로 특성이 분명한 것으로 보임
#최적의 군집분석 수행
km = KMeans(n_clusters=3, random_state=1)
km.fit(df)
labels = km.labels_ #군집 결과 도출
df["cluster"] = labels
df.head()
df.groupby(by="cluster").mean()
import seaborn as sns
sns.pairplot(data=df, hue="cluster")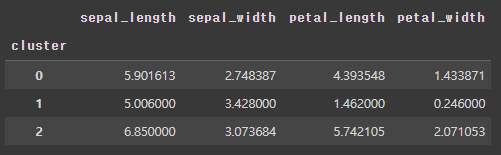
2. 혼합분포 군집분석
- 데이터가 k개의 모집단으로 부터 나왔다는 가정하에 군집분석 실시
- 데이터는 k개의 군집 중 확률이 높은 쪽의 군집에 속하게 됨
- 실생활 데이터는 대부분 정규분포의 형태를 지녀 혼합분포 군집분석이 잘 맞는 경우가 많음
- kmeans에 비해 엄밀한 결과를 얻을 수 있음
- 군집의 크기가 너무 작으면 추정의 정도가 떨어짐
- 데이터가 커지면 EM알고리즘 적용 시 시간/계산비용 증가
- 이상치에 민감하여 전처리 필요
- 유형들의 분포가 정규분포와 차이가 크면 결과가 좋지 않음
- 사용알고리즘: EM(Expectation-Maximization)
- 초깃값 설정: 필요한 모수에 대해 초깃값 설정
- E: 잠재변수 Z의 기대치 계산(X가 특정 군집에 속할 확률을 계산)
- M: 잠재변수 Z의 기대치를 이용해 파라미터 추정
- 수렴조건(최대 가능도가 최대가 되는 지점)이 만족될때까지 E, M을 반복
- from sklearn.mixture.GaussianMixture(parameters)
sklearn.mixture.GaussianMixture
Examples using sklearn.mixture.GaussianMixture: Comparing different clustering algorithms on toy datasets Demonstration of k-means assumptions Density Estimation for a Gaussian mixture GMM Initiali...
scikit-learn.org
예시) iris 데이터에 혼합분포 군집분석 적용
- 데이터정의
- 스케일링 및 군집분석
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
#정규분포로 만들어 주기 위해 스케일링 진행
scaler = StandardScaler()
scaled_df = scaler.fit_transform(df)
#군집분석 실시
gm = GaussianMixture(n_components=3)
gm.fit(scaled_df)
gm_labels = gm.predict(scaled_df)
gm_labels
df["gm_cluster"] = gm_labels
df.groupby(by="gm_cluster").mean()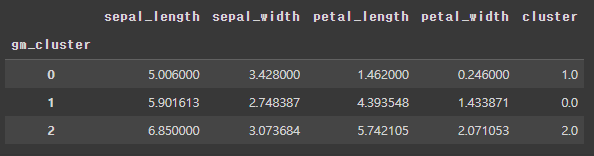
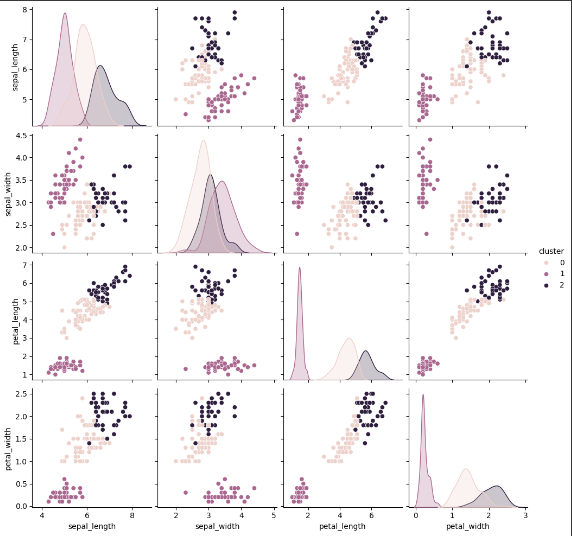
- 시각화
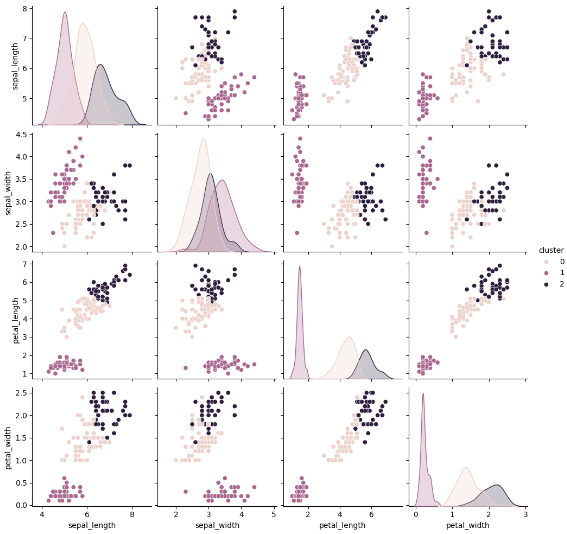
[KMeans와 혼합분포 군집분석 시각화 결과 비교]
- 현데이터에서는 큰 차이가 없는 것으로 나타난다.
- 이론적으로 kmeans는 원형의 데이터, EM은 타원형 데이터를 더 잘 분리하는 것으로 알려져 있다.
- 명확하게 특성이 갈리는 변수는 petal_length, petal_width로 보인다.


'Data Analysis > Statistics' 카테고리의 다른 글
| Python_Statistics_TimeSeries (0) | 2024.03.14 |
|---|---|
| Python_Statistics_Association (0) | 2024.03.13 |
| Python_Statistics_Regression (0) | 2024.03.01 |
| Python_Statistics_Chi-square (0) | 2023.12.15 |
| Python_Statistics_Anova(분산분석) (0) | 2023.12.11 |



