군집분석
- 군집분석이란 객체의 유사성을 측정해서 유사성이 높은 집단끼리 분류하는 통계기법
- 머신러닝 분야에서 이상치 탐지를 위해 사용되기도 함
- 대표적인 비지도 학습
- 계층적 군집분석과 비계층적 군집분석으로 나뉨
[군집분석 vs 요인분석]
| 구분 | 내용 |
| 군집분석 | - 객체간의 상이성을 규명 - 군집의 특성 파악 |
| 요인분석 | - 유사한 변수를 묶어 다중공선성을 줄이기 위함 |
[계층적 군집분석]
- n개의 군집으로 시작해 점차 군집의 개수를 줄여나가는 방식
- 군집의 거리를 계산하는 방법에 따라 연결법이 달라짐
- 모든 객체는 거리 행렬을 통해 가까운 거리의 객체들의 관계를 규명, 군집 개수 선택
- 연결법
| 구분 | 내용 |
| 최단연결법 | - 거리행렬에서 거리가 가장 가까운 데이터끼리 묶어서 군집 형성 |
| 최장연결법 | - 데이터와의 거리를 계산할때 최장거리로 계산 |
| 평균연결법 | - 데이터와의 거리를 계산할때 평균거리로 계산 |
| 중심연결법 | - 두 군집간의 거리를 두 군집의 중심 간 거리로 계산 |
| 와드연결법 | - 군집 내 편차들의 제곱합에 근거를 두고 군집화 - 데이터의 크기가 너무 크지 않다면 가장 많이 사용 - 군집 내 편차는 작고 군집간 편차는 크게 군집화 - 계산량이 많은 단점이 있지만 군집 크기를 비슷하게 만듬 - 해석력이 좋음 |
- scipy.cluster.hierarchy.linkage(parameters)
- scipy.cluster.hierarchy.dendrogram(parameters)
scipy.cluster.hierarchy.linkage — SciPy v1.12.0 Manual
For method ‘single’, an optimized algorithm based on minimum spanning tree is implemented. It has time complexity \(O(n^2)\). For methods ‘complete’, ‘average’, ‘weighted’ and ‘ward’, an algorithm called nearest-neighbors chain is imple
docs.scipy.org
- scipy.cluster.hierarchy.fcluster(parameters)
scipy.cluster.hierarchy.fcluster — SciPy v1.12.0 Manual
An array of length n-1. monocrit[i] is the statistics upon which non-singleton i is thresholded. The monocrit vector must be monotonic, i.e., given a node c with index i, for all node indices j corresponding to nodes below c, monocrit[i] >= monocrit[j].
docs.scipy.org
예시) USArrests정보로 최단, 와드연결법 실시
- 데이터로드 및 전처리
#컬럼명 변경
us.rename(columns={"Unnamed: 0": "state"}, inplace=True)
#컬럼명 소문자로
us.columns = us.columns.str.lower()
us.head()- 최단연결법
- 거리계산은 유클리드거리로 진행
- t값을 기준으로 군집화를 실시했을때 총 6개의 군집이 생기는 것을 확인
- 1개의 state가 1개의 군집으로 모인것도 있음을 확인
#군집분석
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt
#연결방법: 최단연결, 거리계산방법: 유클리드
single = linkage(
us.iloc[:, 1:],
metric="euclidean",
method="single"
)
#시각화
plt.figure(figsize=(10, 7))
dendrogram(
single,
orientation="top",
labels= us["state"].tolist(),
color_threshold=25,
distance_sort="discending"
)
plt.axhline(y=25, color="r", linewidth=1)
plt.show();
- 와드연결법
- 최단 연결법은 군집이 가지고 있는 객체 수가 비슷하지 않아 군집 해결에 어려울 수 있음
- 이런 문제점을 보완하기 위해 와드연결법을 사용
- 유클리디안 거리를 이용해 와드연결법 실시
- t=250선에서 수평축을 그려보면 군집이 3개로 나누어짐을 알 수 있음
- 각 군집의 객체 수도 비슷함을 알 수 있음
#와드연결법 실행
ward = linkage(
us.iloc[:, 1:],
metric="euclidean",
method="ward"
)
plt.figure(figsize=(10, 7))
dendrogram(
ward,
labels=us["state"].tolist(),
distance_sort="descending",
orientation="top"
)
plt.show();
- 군집이 확인 되었으니 fcluster함수를 이용해 각 객체들이 가진 군집번호 데이터화
#각 군집 데이터화
cluster_label = fcluster(ward, 250, criterion="distance")
cluster_label
#원 데이터에 파생변수로 할당된 클러스터 삽입
us["cluster"] = cluster_label
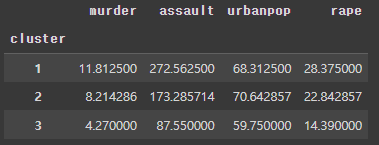
us.head()- 클러스터별 평균 파악
- 1번 클러스터: murder, assault, rape의 평균이 다른 클러스터에 비해 높음
- 2번 클러스터: 전체적으로 중간치의 특성을 보임 urbanpop의 평균이 가장 높음
- 3번 클러스터: 전체적으로 낮은 특성을 보임
[비계층적 군집분석]
- 랜덤하게 군집을 묶어가는 알고리즘
- 거리를 계산하는 방식으로 군집화 실행
- 대표적으로 K-means, DBSCAN, 혼합분포 군집분석이 있음
1. K-means
- 속성의 수가 적은 단순한 데이터에 주로 활용
- 주어진 데이터를 k개로 군집화하며 각 클러스터와 거리차이의 분산을 최소화 하는 방식으로 작동(k개는 연구자 마음)
- 변수가 많을 경우 군집화의 정확도가 떨어짐 > pca(차원축소)를 실시해야 함
- 군집화 알고리즘
- 초깃값 설정: k(군집 수)를 설정할 경우 k개의 데이터를 중심점으로 설정
- 클러스터 설정: 각 데이터로부터 중심점까지를 유클리드 거리로 계산해 해당 가장 가까운 클러스터로 데이터를 재할당
- 각 클러스터의 무게중심을 재설정
- 위의 과정을 반복하다가 중심 변화가 작을때 알고리즘 반복 중지
- 최적의 군집 개수 판단 방법
- 콜린스키 하라바츠 스코어
- 모든 클러스터에 대한 클러스터 간 분산과 클러스터 내 분산의 합의 비율
- 높을 수록 좋음
- 엘보우
- 컬러스터 내 오차제곱합(SSE)을 개수마다 비교하는 방법
- 반복문을 통해 클러스터 개수(k)를 늘려가며 SSE값을 비교
- 기울기가 소실되는 구간을 elbow로 판단하고 그 순간을 최적의 클러스터 개수로 판단
- 콜린스키 하라바츠 스코어
예시) iris데이터를 활용한 군집 분석
- 데이터정의
- 최적의 군집 수 결정
- 하라바츠스코어
- 3개가 최적의 군집수로 보임
- 하라바츠스코어
#군집 수 결정(하라바츠스코어)
from sklearn.metrics import calinski_harabasz_score
import warnings
warnings.filterwarnings("ignore")
for k in range(2, 10):
km = KMeans(n_clusters=k, random_state=1)
km.fit(df)
labels = km.labels_
print(k, calinski_harabasz_score(df, labels))
'''
2 513.9245459802768
3 561.62775662962
4 530.4871420421675
5 495.54148767768777
6 473.5154538824768
7 443.84523107907245
8 440.59767319067873
9 407.0468400265113
'''
-
- 엘보우
- 시각화 결과 2개에서 3개가 기울기가 완만해 지는 지점임
- 엘보우
#엘보우 확인
import matplotlib.pyplot as plt
sses = []
for k in range(1, 11):
km = KMeans(n_clusters=k, random_state=1)
km.fit(df)
sses.append(km.inertia_) #kmeans의 sse 확인 메서드
plt.plot(range(1, 11), sses, marker="o")
plt.xlabel("n_clusters")
plt.ylabel("SSE")
plt.show();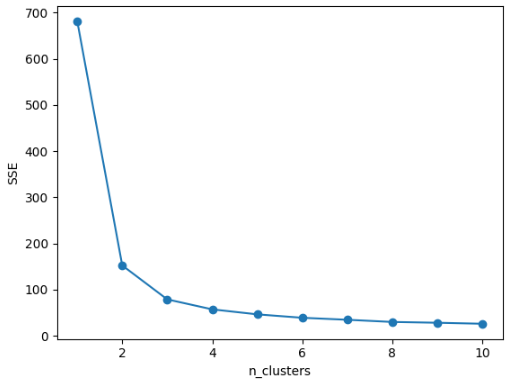
- 군집분석 실시
- k=3으로 군집분석 실시 후 groupby, 시각화
- 변수별로 특성이 분명한 것으로 보임
#최적의 군집분석 수행
km = KMeans(n_clusters=3, random_state=1)
km.fit(df)
labels = km.labels_ #군집 결과 도출
df["cluster"] = labels
df.head()
df.groupby(by="cluster").mean()
import seaborn as sns
sns.pairplot(data=df, hue="cluster")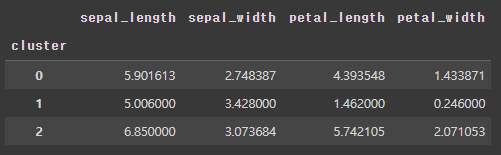
2. 혼합분포 군집분석
- 데이터가 k개의 모집단으로 부터 나왔다는 가정하에 군집분석 실시
- 데이터는 k개의 군집 중 확률이 높은 쪽의 군집에 속하게 됨
- 실생활 데이터는 대부분 정규분포의 형태를 지녀 혼합분포 군집분석이 잘 맞는 경우가 많음
- kmeans에 비해 엄밀한 결과를 얻을 수 있음
- 군집의 크기가 너무 작으면 추정의 정도가 떨어짐
- 데이터가 커지면 EM알고리즘 적용 시 시간/계산비용 증가
- 이상치에 민감하여 전처리 필요
- 유형들의 분포가 정규분포와 차이가 크면 결과가 좋지 않음
- 사용알고리즘: EM(Expectation-Maximization)
- 초깃값 설정: 필요한 모수에 대해 초깃값 설정
- E: 잠재변수 Z의 기대치 계산(X가 특정 군집에 속할 확률을 계산)
- M: 잠재변수 Z의 기대치를 이용해 파라미터 추정
- 수렴조건(최대 가능도가 최대가 되는 지점)이 만족될때까지 E, M을 반복
- from sklearn.mixture.GaussianMixture(parameters)
sklearn.mixture.GaussianMixture
Examples using sklearn.mixture.GaussianMixture: Comparing different clustering algorithms on toy datasets Demonstration of k-means assumptions Density Estimation for a Gaussian mixture GMM Initiali...
scikit-learn.org
예시) iris 데이터에 혼합분포 군집분석 적용
- 데이터정의
- 스케일링 및 군집분석
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
#정규분포로 만들어 주기 위해 스케일링 진행
scaler = StandardScaler()
scaled_df = scaler.fit_transform(df)
#군집분석 실시
gm = GaussianMixture(n_components=3)
gm.fit(scaled_df)
gm_labels = gm.predict(scaled_df)
gm_labels
df["gm_cluster"] = gm_labels
df.groupby(by="gm_cluster").mean()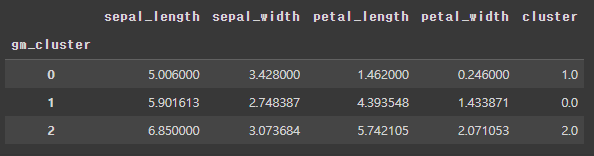
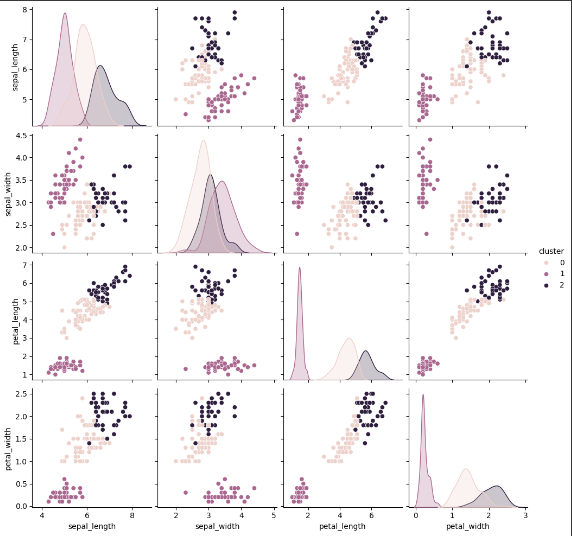
- 시각화
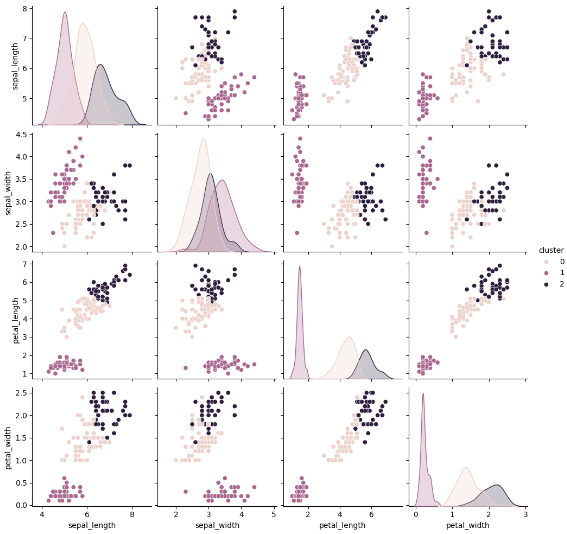
[KMeans와 혼합분포 군집분석 시각화 결과 비교]
- 현데이터에서는 큰 차이가 없는 것으로 나타난다.
- 이론적으로 kmeans는 원형의 데이터, EM은 타원형 데이터를 더 잘 분리하는 것으로 알려져 있다.
- 명확하게 특성이 갈리는 변수는 petal_length, petal_width로 보인다.


'Data Analysis > Statistics' 카테고리의 다른 글
| Python_Statistics_TimeSeries (0) | 2024.03.14 |
|---|---|
| Python_Statistics_Association (0) | 2024.03.13 |
| Python_Statistics_Regression (0) | 2024.03.01 |
| Python_Statistics_Chi-square (0) | 2023.12.15 |
| Python_Statistics_Anova(분산분석) (0) | 2023.12.11 |



