단순선형회귀(Simple Linear Regression)
- 종속변수에 대한 선형함수를 만들어 예측하는 알고리즘
- 독립변수가 하나인 경우 특정 직선을 학습
$$ y = \beta_0 + \beta_1*x $$
- 입력 특성의 가중치($\beta_1 *x$) 합과 편향($\beta_0$)을 더해 예측을 수행
- 선형 회귀 모델을 이용해 학습데이터세트에 가장 적합하도록 모델 파리미터를 설정하는 과정을 '모델을 학습시킨다'라고 함
- 선형회귀 모델을 잘 학습시키기 위해 MSE(평균제곱오차)를 최소화하는 파라미터를 찾아야 함
- 통계방식: 정규방정식을 사용해 MSE를 최소화
- 머신러닝: 경사하강법을 사용해 MSE를 최소화
정규방정식
- 정규방정식을 통해 MSE값을 최소로 하는 파라미터를 얻을 수 있음
- 최소자승법(Least Squares Method)을 코드로 구현 가능
- scikit-larn 패키지에서 함수 LinearRegression 사용
- 최소자승법을 사용한 OLS(Ordinary Least Squares)방식으로 모델 구현
- w=(w1, w2, ....., wp)를 사용해 모델을 피팅하여
- 데이터 세트와 예측된 대상간의 잔차 제곱합을 최소화함
- sklearn.linear_model.LinearRegression(*, fit_intercept={default:True}, normalize={default=False} , copy_X={default:False}, n_jobs=int({default=None}), positive={default:False})
| Parameter | |
| fit_intercept | - 모델에서 절편을 계산할지 여부 계산 - False는 절편을 사용하지 않음(데이터가 원점을 지나 중앙에 위치) |
| normalize | - 정규화 진행 여부 - True일 경우 X에서 평균을 빼고 L2-norm으로 나누어 회귀 전에 정규화됨 - 표준화 진행하고 싶으면 default(False)로 두고 StandardScaler를 사용하여 표준화 진행 후 fit() |
| copy_X | - True일 경우 X가 복사됨 |
| n_jobs | - 계산 작업 횟수 |
| positive | - True일 경우 계수가 양수가 됨 |
| Property | |
| coef_ | - 추정된 계수(array형태로 반환) |
| rank_ | - 행렬 X의 rank |
| singular_ | - 행렬 X의 특이값 |
| intercept_ | - 모델의 독립항($\beta_0$) |
| Method | |
| fit(X, y) | - 모델학습 - X: train data, 2차원 입력 - y: train target data, 1차원 입력 |
| get_params([deep]) | - 선형 회귀 모델의 매개변수 가져옴 - deep: bool형태로 가져옴 - 값에 매치되는 파라미터의 이름을 딕셔너리 형태로 반환 |
| predict(X) | - 선형 모델을 사용해 예측 - X: test data, 2차원 입력 - 예측값을 array로 반환 |
| score(X, y) | - 예측의 결정계수 반환 - X: test data - y: test target data, - 결정계수를 float으로 반환 |
예시1) insurance 데이터 활용 선형회귀 모델 구현
- 나이(Age)와 의료비용 사이의 선형 모델을 생성한다.
- 데이터를 로드하고 기본정보를 파악한다.
- 모델을 생성하기에 앞서 나이(age)와 의료비용(charges)변수 간의 선형성을 확인한다.
- 두 변수간 선형성이 나타나는 것이 확인된다.
#---------- kaggle insurance 데이터 로드
#---------- 선형성 확인
sns.scatterplot(data=data, x="age", y="charges")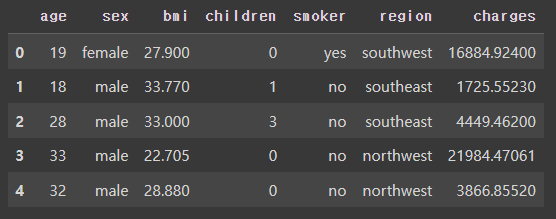
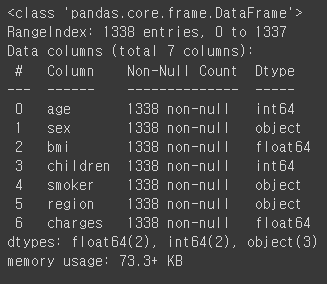
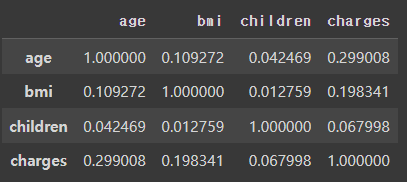
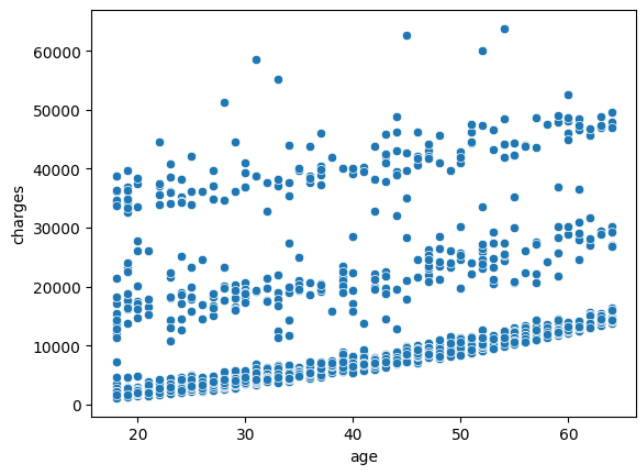
데이터정보, 선형성, 상관성 확인
- 회귀모델 생성
- 결과에 따른 회귀식은 다음과 같다.
- $charges = 3165.88 + 257.72*age$
- 결정계수는 8%로 매우 낮음
from sklearn.linear_model import LinearRegression
#---------- 모델생성 및 학습
lr = LinearRegression()
lr.fit(data[["age"]], data[["charges"]]) #2차원으로 입력
#---------- 결과
print(f"절편: {lr.intercept_}")
print(f"회귀계수: {lr.coef_}")
print(f"결정계수: {lr.score(data[['age']], data[['charges']])}")
# 절편: [3165.88500606]
# 회귀계수: [[257.72261867]]
# 결정계수: 0.08940589967885804
- 새로운 데이터 샘플을 회귀 모형에 입력하여 나이에 따른 의료비용 예측
- 결과 15세는 7031.724원 / 61세는 18886.96원을 지출한다고 해석 가능하다.
#새로운 데이터 입력하여 예측값 출력
new_X = [[15], [61]]
pred_y = lr.predict(new_X)
print(pred_y)
#결과
#[[ 7031.72428607] [18886.96474474]]
- 이를 시각화 해보면 다음과 같다.
#----------- 시각화
fig = plt.figure()
plt.plot(data["age"], data["charges"], "b.")
plt.plot(new_X, pred_y, "r-")
plt.show();
'Data Analysis > Machine Learning' 카테고리의 다른 글
| Python_ML_Supervised_KNN (1) | 2024.02.28 |
|---|---|
| Python_ML_Supervised_SVM (0) | 2024.01.03 |
| Python_ML_Supervised_Multiple Regression (0) | 2024.01.02 |
| Python_ML_Supervised_Polynomial Regression (0) | 2024.01.02 |
| Python_ML_Supervised_Logistic Regression (0) | 2023.12.18 |



