Data Analysis/Machine Learning
Python_ML_Supervised_Multiple Regression
mansoorrr
2024. 1. 2. 13:26
다중회귀(Multiple Regression)
- 독립변수가 여러개 있는 회귀분석을 의미
- 여러개의 독립변수가 종속변수에 영향을 미치는 경우 다중회귀모형으로 데이터 표현 가능
$$ \widehat{Y}= \sum_{i=1}^n\beta_ix_i $$
- 최적의 모델을 결정하기 위해 다양한 방법으로 변수를 선택
- 모델이 복잡해지면 과대적합이 발생할 가능성이 있어 다양한 규제를 적용해 가중치를 제한
- 변수선택법을 통한 다항회귀 모델
- 다중선형모델의 성능을 높이기 위해 독립변수의 부분집합을 선택하는 방법
- 전진선택법과 후진선택법으로 나뉨
- 통계 기법에서 사용됨
| 구분 | 내용 |
| 전진선택법 | 단순 선형회귀에서 변수를 하나씩 추가 가며 모델의 정확도 높이는 방법 |
| 후진제거법 | 모든 변수 추가하고 유의하지 않은 변수들 제거하며 모델의 성능을 높이는 방법 |
| 단계적 선택법 | 변수를 추가 제거하며 모델의 성능을 높이는 방법 |
- 규제를 통한 다항회귀 모델
- 변수선택법의 대안으로 계수추정치들을 제한하거나 규칙화 하는 기법을 적용하여 독립변수를 모두 포함시킴
- 규칙에 따라 계수 추정치들을 0으로 수축하는 방식으로 다중회귀모델의 성능 높임
- 규제 방법으로 릿지(L1), 라쏘(L2), 엘라스틱넷 이 있음
[릿지(Ridge)]
- MSE(training accuracy)에 Genalization accuracy(일반화: 규제항)항을 추가하여 overfitting을 방지한다.
$$ RidgeMSE(\beta) = MSE(\beta) + a1/2\sum_{i=1}^n\beta^2_i $$
- a = 0이면 선형회귀의 mse와 동일하다
- a가 커질수록 규제가 강하게 들어가며 variance가 감소하게 되고 overfitting에서 벗어나게 된다
- 변수선택법에 비해 속도도 빠르다.
- 크기가 큰 변수를 우선적으로 줄이는 경향이 있음
- sklearn.linear_model.Ridge(parameters)
| Parameter | |
| alpha | - default=1.0 - 정규화 강도를 정하는 값 - 소수점이어야 하며, 값이 커질수록 정규화의 강도가 세짐 |
| fit_intercept | - default=True - 절편 계산할지 여부 - False: 절편을 사용하지 않는 모델로 계산 |
| normalize | - default=False - True: (X-평균) / L2-norm 회귀 전에 정규화 함. - 보통 False로 놓고 외부에서 StandardScaler사용해서 정규화 진행 |
| positive | - default=False - True: 계수가 양수가 됨 |
| copy_X | - default=True(X복사) - False: X 덮어씀 |
| Property | |
| coef_ | - 추정된 회귀 계수 |
| intercept_ | - 절편 |
| Method | |
| fit(X, y) | - 학습 - X: train data( 2차원) - y: train target data |
| get_params([deep]) | - 모델의 파라미터 가져옴 - 딕셔너리 형태로 반환 |
| predict(X) | - 모델을 사용해 예측 - X: test data(2차원) |
| score(X, y) | - 모델의 결정계수(모델성능) - X: test data(2차원) - y: test target data |
예제 1) 당뇨 데이터를 통해 릿지 회귀 수행
- 릿지 회귀를 수행하고 a값에 따라 회귀계수의 변화를 시각화 한다.
- sklearn에서 제공하는 diabetes 데이터를 로드하여 기본 정보를 확인한다.
- 442개 데이터에 11개 변수이다.
- 변수별 결측치는 없다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_diabetes
# 데이터 로드
data = load_diabetes()
df = pd.DataFrame(data.data, columns=data.feature_names)
df["target"] = data.target
print(df.shape)
df.head()

- 데이터를 분할하고 Ridge 모델의 alpha값을 조정해서 회귀계수를 산출한다.
- a값은 np.logspace를 통해 생성한다.
from sklearn.linear_model import Ridge
#---------- 데이터 분할
X = df.drop(["target"], axis=1)
y = df["target"]
#---------- a정의
alpha = np.logspace(-3, 1, 5)
alpha
#---------- 회귀실시
ridge_coef = []
for a in alpha:
ridge = Ridge(alpha=a)
ridge.fit(X, y)
ridge_coef.append(ridge.coef_)
# a값에 따른 데이터 프레임 생성
ridge_df = pd.DataFrame(ridge_coef, columns=X.columns, index=alpha)
ridge_df
- a값의 변화에 따라 회귀계수가 변화하는 모습을 확인한다.
- a값이 커지면 정규화 강도가 커지므로 회귀계수가 0에 수렴하게 되고
- a값이 0이면 mse와 동일하다
#a값 변화에 따라 시각화
plt.figure()
plt.semilogx(ridge_df)
plt.legend(labels=ridge_df.columns, bbox_to_anchor=(1,1))
plt.title("Ridge")
plt.xlabel("alpha")
plt.ylabel("Coef")
plt.axhline(y=0, linestyle="--", color="black", linewidth=2)
plt.show();
- 회귀분석과 비교한다.
- a가 0이면 mse를 활용한 모델의 계수와 비슷해 짐을 확인할 수 있다.
lr = LinearRegression()
lr.fit(X, y)
linear_coef = lr.coef_
plt.axhline(y=0, linestyle="--", linewidth=2, color="black")
plt.plot(ridge_df.loc[0.001], "^-", linewidth=3, label="Ridge alpha = 0.001")
plt.plot(ridge_df.loc[0.010], "o-", label="Ridge alpha = 0.010")
plt.plot(ridge_df.loc[0.100], ":", label="Ridge alpha = 0.100")
plt.plot(ridge_df.loc[1.000], "v-", label="Ridge alpha = 1.000")
plt.plot(ridge_df.loc[10.000], "*--", label="Ridge alpha = 10.000")
plt.plot(linear_coef, "r-", linewidth=3, label="LinearRegression")
plt.xlabel("x")
plt.ylabel("coef")
plt.legend(bbox_to_anchor=(1,1))
plt.show();
[라쏘(Lasso)]
- 변수의 개수가 매우 많은 데이터로 릿지 모델을 실행시키면 결과 해석의 문제가 있음
$$ RidgeMSE(\beta) = MSE(\beta) + a\sum_{i=1}^n|{\beta_i}| $$
- 라쏘의 수축패널티는 $\beta_i$가 0에 가까울때 작으므로 $/beta_i$의 추정치를 0으로 수축하는 효과를 줌
- 단, a가 충분히 클때, 계수 추정치들의 일부를 0이 되게 할 수 있음(덜 중요한 변수는 가중치를 제거할 수 있다는 점이 릿지와의 차이점)
- 즉 회소(sparse) 모델을 만들 수 있음
- 변수 간 상관관계가 높을 경우 ridge에 비해 예측성능 떨어짐
- sklearn.linear_model.Lasso(parameters)
| Parameter(릿지와 동일) | |
| alpha | - default=1.0 - 정규화 강도를 정하는 값 - 소수점이어야 하며, 값이 커질수록 정규화의 강도가 세짐 - 0일 경우 OLS기반 회귀와 동등한 결과 도출 |
| fit_intercept | - default=True - 절편 계산할지 여부 - False: 절편을 사용하지 않는 모델로 계산 |
| normalize | - default=False - True: (X-평균) / L2-norm 회귀 전에 정규화 함. - 보통 False로 놓고 외부에서 StandardScaler사용해서 정규화 진행 |
| positive | - default=False - True: 계수가 양수가 됨 |
| copy_X | - default=True(X복사) - False: X 덮어씀 |
| Property(릿지와 동일) | |
| coef_ | - 추정된 회귀 계수 |
| intercept_ | - 절편 |
| Method(릿지와 동일) | |
| fit(X, y) | - 학습 - X: train data( 2차원) - y: train target data |
| get_params([deep]) | - 모델의 파라미터 가져옴 - 딕셔너리 형태로 반환 |
| predict(X) | - 모델을 사용해 예측 - X: test data(2차원) |
| score(X, y) | - 모델의 결정계수(모델성능) - X: test data(2차원) - y: test target data |
예시 1) 당뇨 데이터를 통해 라쏘 회귀 수행
- 릿지 때와 동일하게 a값을 생성하여 a별 lasso를 적용한다.
- a는 np.logspace를 사용한다.
- 모델을 만들고 a별 도출된 회귀계수를 확인한다.
- 데이터프레임으로 봤을때도 특정 변수들의 회귀계수를 0으로 만드는 것을 확인할 수 있다.
- 시각화 해보면 a값이 커질수록 회귀계수가 점점 0이 되는 것을 확인 가능하다.
from sklearn.linear_model import Lasso
lasso_alpha = np.logspace(-3, 1, 5)
lasso_coef = []
for alpha in lasso_alpha:
lasso = Lasso(alpha=alpha)
lasso.fit(X, y)
lasso_coef.append(lasso.coef_)
lasso_df = pd.DataFrame(lasso_coef, columns=X.columns, index=lasso_alpha)
lasso_df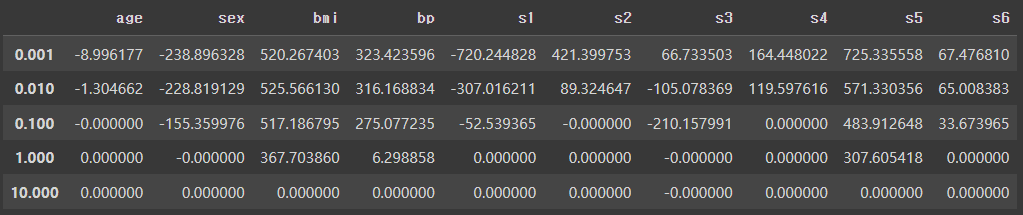

- MSE를 활용한 LinearRegression과 비교 진행
- alpha가 작은 라쏘 모델의 회귀 계수는 MSE를 활용한 LinearRegression의 회귀계수와 비슷하다.
- 또한 alpha가 커지면서 회귀계수는 0이 되었다.
lr = LinearRegression()
lr.fit(X, y)
lr_coef = lr.coef_
plt.plot(lasso_df.loc[0.001], "^-", label="Lasso alpha = 0.001")
plt.plot(lasso_df.loc[0.010], "o-", label="Lasso alpha = 0.010")
plt.plot(lasso_df.loc[0.100], "*-", label="Lasso alpha = 0.100")
plt.plot(lasso_df.loc[1.000], ":", label="Lasso alpha = 1.000")
plt.plot(lasso_df.loc[10.000], "^--", label="Lasso alpha = 10.000")
plt.plot(lr_coef, label="LinearRegression", linewidth=2)
plt.axhline(y=0, linestyle="--", linewidth=2, color="black")
plt.legend(bbox_to_anchor=(1,1))
plt.show();
[엘라스틱넷(Elasticnet)]
- 엘라스틱넷은 릿지와 라쏘를 절충한 알고리즘
- 수축패널티는 릿지와 라쏘를 단순히 더함
- 혼합비율 r을 활용해 조절(r=0이면 릿지와 같고, r=1이면 라쏘와 같음)
- sklearn.linear_model.ElasticNet(parameters)
| Parameter | |
| alpha | - default=1.0 - 정규화 강도를 정하는 값 - 소수점이어야 하며, 값이 커질수록 정규화의 강도가 세짐 - 0일 경우 OLS기반 회귀와 동등한 결과 도출 |
| fit_intercept | - default=True - 절편 계산할지 여부 - False: 절편을 사용하지 않는 모델로 계산 |
| normalize | - default=False - True: (X-평균) / L2-norm 회귀 전에 정규화 함. - 보통 False로 놓고 외부에서 StandardScaler사용해서 정규화 진행 |
| positive | - default=False - True: 계수가 양수가 됨 |
| copy_X | - default=True(X복사) - False: X 덮어씀 |
| Property | |
| coef_ | - 추정된 회귀 계수 |
| intercept_ | - 절편 |
| Method | |
| fit(X, y) | - 학습 - X: train data( 2차원) - y: train target data |
| get_params([deep]) | - 모델의 파라미터 가져옴 - 딕셔너리 형태로 반환 |
| predict(X) | - 모델을 사용해 예측 - X: test data(2차원) |
| score(X, y) | - 모델의 결정계수(모델성능) - X: test data(2차원) - y: test target data |
예시 1) 당뇨데이터를 통해 엘라스틱넷 회귀 수행
- alpha값 조정하여 위와 동일하게 진행
- elasticnet또한 alpha가 증가하면서 0으로 수렴하는 것을 확인할 수 있다.
from sklearn.linear_model import ElasticNet
ela_alpha = np.logspace(-3, 1, 5)
ela_coef = []
for alpha in ela_alpha:
ela = ElasticNet(alpha=alpha)
ela.fit(X, y)
ela_coef.append(ela.coef_)
ela_df = pd.DataFrame(ela_coef, columns=X.columns, index=ela_alpha)
plt.semilogx(ela_df)
plt.axhline(y=0, color="black", linewidth=2, linestyle="--")
plt.title("ElasticNet")
plt.xlabel("alpha")
plt.ylabel("coef")
plt.legend(labels=ela_df.columns, bbox_to_anchor=(1,1))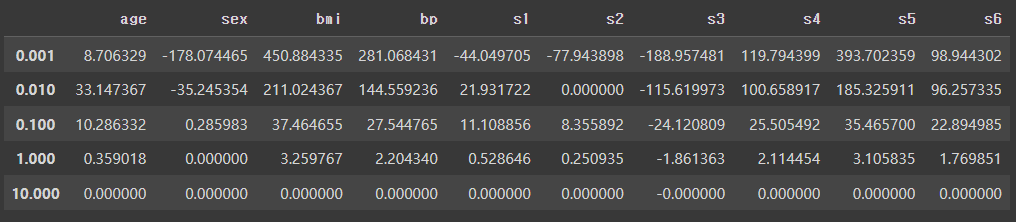

- LinearRegression과 비교를 진행한다
- alpha값이 커지면서 회귀계수는 0이 된다.
- alpha값이 0이면 LinearRegression과 비슷한 회귀계수를 갖는다.
plt.plot(ela_df.loc[0.001], "^-", label="Elastic alpha = 0.001")
plt.plot(ela_df.loc[0.010], "o-", label="Elastic alpha = 0.010")
plt.plot(ela_df.loc[0.100], "*-", label="Elastic alpha = 0.100")
plt.plot(ela_df.loc[1.000], ":", label="Elastic alpha = 1.000")
plt.plot(ela_df.loc[10.000], "^--", label="Elastic alpha = 10.000")
plt.plot(lr_coef, label="LinearRegression", linewidth=2)
plt.axhline(y=0, linestyle="--", linewidth=2, color="black")
plt.legend(bbox_to_anchor=(1,1))
plt.show();