Python_ML_Supervised_Logistic Regression

로지스틱회귀(Logistic Regression)

• 선형 모델을 분류하는데 사용해 샘플이 특정 클래스에 속할 확률을 추정 가능
• 이름은 회귀지만 종속변수가 범주형인 경우 사용
• 종속변수가 특정 범수에 속하는 확률을 모델링함
• 시그모이드(로지스틱)함수
  • 로지스틱 회귀는 선형회귀처럼 $y=\beta_0 + \beta_1X$로 표현해야 하는데 y가 범주형 변수이기 때문에 저렇게 표현하면 예측이 맞지 않는다.
  • 따라서 모든 값에 0 또는 1사이의 값을 제공하는 함수를 사용해야 함
  • X가 아주 큰 음수일때 0이 되고 아주 큰 양수일때 1이 되도록 바꿔줌
• 승산비(Odds)
  • 실패(1-p)에 비해 성공(p)할 확률
  • $p/(1-p)$
  • $P(Y=1|X)$ 가 1에 가까워 질수록 Odds가 무한대로 발산하는 한계가 있음 
  • 이를 극복하기 위해 log를 씌움
    • log(Odds)는 범위가 $-\infty < log(Odds) < \infty$로 변경됨
    • X가 음수일때는 y가 0에서 0.5 이하인 값을 갖고, X가 양수일때는 Y가 0.5 이상에서 1이하인 값을 반환
    • 즉, 성공확률 0.5를 기준으로 X값이 나뉘게 됨
    • 이를 활용해 독립변수에 로짓반응을 적용하여 모델링 하는 것이 로지스틱 회귀
• 훈련 및 비용함수
  • 로지스틱 회귀 모델의 학습목적은 양성 샘플(y=1)에 대해서는 높은 확률을 추정하고, 음성 샘플(y=0)에 대해서는 낮은 확률을 추정하는 모델의 파라미터를 찾는것
  • 이를 위해 최대우도추정법(MLE: Maximum Likelihood Function)을 사용
• sklearn.linear_model.LogisticRegression(parameters)

Parameter
penalty	- default: l2 - 패널티에 적용할 norm결정 - l2, l1, elasticnet 적용 가능
dual	- default: False - Dual formulation을 실행할지 여부를 나타냄 - n_sample이 n_feature보다 클 경우 False를 추천
tol	- default: 1e-4 - 중지기준에 대한 허용 오차
C	- default: 1.0 - 정규화 강도의 역수
fit_intercept	- default: True - bias or 절편을 추가해야 하는지 여부
class_weigth	- default: None - 클래스와 관련된 가중치 - 지정하지 않으면 모든 클래스의 가중치는 1
random_state	- default: None
solver	- default: lbfgs - 최적화 문제를 푸는 해를 구할 때 사용하는 알고리즘 설정 - 데이터 세트의 크기가 작으면 liblinear - 다중클래스에서는 newton-cg, sag, saga, libfgs사용
multi_class	- default: auto - 클래스 타입 설정 - auto: 자동, ovr: 2진분류, multinomial: 다중분류
verbose	- default: 0 - 과정 확인
l1_ratio	- default: None - penalty가 elasticnet일 경우만 사용

Property
classes_	- 분류기에서 라벨링된 클래스
coef_	- feature에 할당된 가중치
intercept_	- 선형모델의 절편
n_iter	- 중지 기준에 도달하기 전까지 실제 반복 횟수

Method
fit(X, y)	- 학습 - X: train data( 2차원) - y: train target data
get_params([deep])	- 모델의 파라미터 가져옴 - 딕셔너리 형태로 반환
predict(X)	- 모델을 사용해 예측 - X: test data(2차원)
score(X, y)	- 모델의 결정계수(모델성능) - X: test data(2차원) - y: test target data
predict_proba(X)	- X: test data(2차원) - 샘플데이터가 클래스에 속할 확률
predict_log_proba(X)	- X: test data(2차원) - 샘플데이터가 클래스에 속할 로그확률
decision_function	- X에 대해 예측한 y가 양수인지 음수인지 - 예측한 y가 Hyperplane(0)과 얼마나 떨어져 있는지

 

 

예시 1) Kaggle bodyPerformance 데이터를 활용한 로지스틱 회귀(2진 분류) 구현

• 13393개데이터이며 12개의 컬럼을 가지고 있다.
• 종속변수인 class는 범주형 변수이다.
• 독립변수들중 gender를 제외한 나머지는 수치형 변수이다.
• gender, class의 분포는 사진과 같다.

 

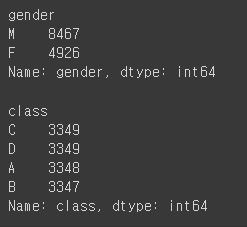
• gender를 남자=0, 여자=1로 변경한다.
• 2진분류를 수행하기 위해 class가 A에 속하면 1로, 나머지는 0으로 변경한다.

body["gender"] = np.where(body["gender"]=="M", 0, 1) #gender변경
body["class_1"] = np.where(body["class"]=="A", 1, 0) #class변경

obj_cols = ["gender", "class_1"]
for col in obj_cols:
  print(f"\n{col}")
  print(body[col].value_counts())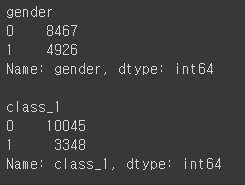

변경 완료된 후 분포

 

• 데이터를 독립변수와 종속변수로 분리한다.
• 학습용과 테스트용으로 7:3 분할을 실시한다.

from sklearn.model_selection import train_test_split

#데이터 분할
remove_cols = ["class", "class_1"]
x_cols = body.columns.difference(remove_cols)

X = body[x_cols]
y = body["class_1"]


x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=1)
print(f"x_train shape: {x_train.shape}")
print(f"y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape}")
print(f"y_test shape: {y_test.shape}")

# x_train shape: (9375, 11)
# y_train shape: (9375,)
# x_test shape: (4018, 11)
# y_test shape: (4018,)

 

• x_train, y_train을 통해 학습한 결과를 확인해 본다.
• 분류한 결과와 왜 그렇게 분류했는지를 알아본다.
• predict를 통해 분류결과를 확인하고
• predict_proba를 통해 분류결과의 이유를 확인한다. 2차원 array로 반환된다.
• decision_fuction을 통해 0과 떨어진 결과를 확인한다.
• 확인 결과
  • org_y와 x_train_pred를 보면 맞게 분류한것도 있고 틀리게 분류한것도 있다.
  • x_train_proba0과 x_train_proba1은 predict_proba의 결과이다. 0은 0으로 분류할 확률, 1은 1로 분류할 확률을 나타낸다.
  • 0으로 분류했을때의 확률이 1로 분류했을때의 확률보다 높은 경우 0으로 분류한다.
  • 반대로 1로 분류했을때의 확률이 높으면 1로 분류하는 것을 알 수 있다.
  • 0으로 분류된 경우 decision_function은 음수값을 가지며 확률이 높을수록 값도 크다.

x_train_pred = logr.predict(x_train) # x_train으로 예측한 결과 반환
x_train_proba = logr.predict_proba(x_train) # x_train으로 예측한 결과에 대한 확률 반환
cs = logr.decision_function(x_train) # 0을 기준으로 양수인지 음수인지 확인

compare_df = pd.DataFrame({"org_y": y_train})

compare_df["x_train_pred"] = x_train_pred
compare_df[["x_train_proba0", "x_train_proba1"]] = x_train_proba
compare_df["decision_function"] = cs
compare_df.head()

 

• decision_function에 따른 확률값을 매칭시킨다
• decision_function의 크기가 작아지면 0으로 분류할 확률이 커지고, 커지면 1로 분류할 확률이 커지는 것을 볼 수 있다
• x=0, y=0.5를 기준으로 1과 0으로 나뉜다

import matplotlib.pyplot as plt
import seaborn as sns
import warnings

warnings.filterwarnings("ignore")

plt.axhline(y=0.5, linewidth=1, linestyle="--", color="black")
plt.axvline(x=0, linewidth=1, linestyle=":", color="black")
plt.plot(compare_df["decision_function"], compare_df["x_train_proba0"], "r.", linewidth=0.3, label="class0 proba")
plt.plot(compare_df["decision_function"], compare_df["x_train_proba1"], "b*", linewidth=0.3, label="class1 proba")
plt.legend(loc="upper left")
plt.show();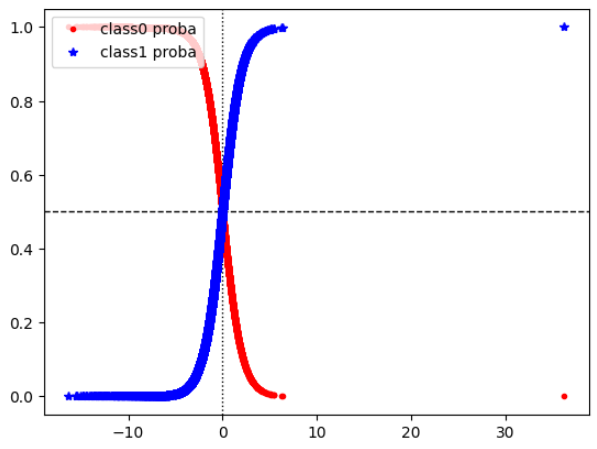

 

• 혼동행렬과 정확도 등 평가 지표들을 확인한다.
• 잘못 예측한 갯수는 620개 정도 된다.
• 정확도는 84.5%로 나타나고 나머지 지표들은 준수한 수준이다.
• auc값을 확인한 결과 0.91로 나타난다.

#---------- 정확도 파악
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score

pred = logr.predict(x_test) #예측

cfm = confusion_matrix(y_test, pred)
acc = accuracy_score(y_test, pred)
prc = precision_score(y_test, pred)
rc = recall_score(y_test, pred)
f1 = f1_score(y_test, pred)

print(f"\n[confusion matrix]\n {cfm}")
print(f"\n[accuracy]: {acc}")
print(f"[precision]: {prc}")
print(f"[recall]: {rc}")
print(f"[f1 score]: {f1}")

#---------- ROC curve 확인
from sklearn.metrics import RocCurveDisplay
RocCurveDisplay.from_estimator(logr, x_test, y_test)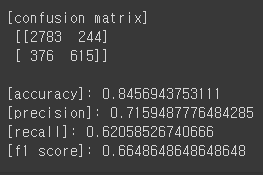

 

 

예시2) Kaggle bodyPerformance 데이터를 활용한 소프트맥스 회귀(다중분류) 구현

• 소프트맥스 함수
  • 클래스에 대한 점수를 계산하고 그 점수에 소프트맥스 함수를 적용해 각 클래스의 확률을 추정
  • LogisticRegression의 multi_class를 multinomial로 바꾸면 소프트맥스 회귀 사용 가능
  • solver도 소프트맥스 회귀를 적용가능하도록 알고리즘 설정해야 함
• 혼동행렬도 4개 클래스로 분리되서 나타남
• 정확도는 60%가 나타남
• 예측결과와 예측확률을 확인해본 결과 확률이 가장 높은 클래스로 분류함을 확인 가능

#---------- 전처리
class_mapping = {
    "A": 0,
    "B": 1,
    "C": 2,
    "D": 3
}
body["class_2"] = body["class"].map(class_mapping)

#---------- 데이터 분할
y = body["class_2"]
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=1)
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)

#---------- 데이터 정의
sm_logr = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10) # 다중분류 지정


#--------- 데이터 평가
sm_pred = sm_logr.predict(x_test)
sm_cfm = confusion_matrix(y_test, sm_pred)
sm_acc = accuracy_score(y_test, sm_pred)

print(sm_cfm)
print(sm_acc)

#--------- 분류 결과에 대한 확인
sm_pred[0] # 3번
sm_proba = sm_logr.predict_proba(x_test)
sm_proba[0, :] #array([0.00510206, 0.07849222, 0.22014509, 0.69626064])
#3번째 레이블의 확률이 가장 높은것을 확인할 수 있다.